Basic Concepts: Simple Interest & Compound Interest | Quantitative Aptitude (Quant) - CAT PDF Download
| Table of contents |

|
| What are Interest Rates? |

|
| Simple Interest |

|
| Solved examples on Simple Interest |

|
| Compound Interest |

|
| Solved Examples on Compound Interest |

|
| Depreciation of Value |

|
| Population Based Question |

|
What are Interest Rates?
- Interest rates are very powerful and intriguing mathematical concepts. Our banking and finance sector revolves around interest rates. One minor change in these rates could have tremendous and astonishing impacts over the economy. But why?
- Before determining the reason of this why, let’s first know what is interest and these interest rates?
Interest is the amount charged by the lender from the borrower on the principal loan sum. It is basically the cost of renting money. And, the rate at which interest is charged on the principal sum is known as the interest rate.
The rate at which interest is charged depends on two factors:
- The value of money doesn’t remain same over time. It changes with time. The net worth of ₹ 100 today will not be same tomorrow i.e. If 5 pens could be bought presently with a INR 100 note then in future, maybe only 4 pens can be bought with the same ₹ 100 note. The reason behind this the inflation or price rise. So, the interest rate includes this factor of inflation
- The credibility of the borrower, if there is more risk and chance of default on the borrower’s part then more interest will be charged. And, if there is less chance of payment failure on the part of borrower then the rate of interest would be lower.
Since change in interest rate has a chain effect in the market, it has a great deal of importance in the study of market, finance, and economy. And that’s why, forms an integral part of the curriculum in the MBA programs.
Types of Interest Rates
Interests are of two types:
- Simple Interest
- Compound Interest

Simple Interest
Simple interest is the interest calculated on the original amount borrowed for the entire duration, using a fixed interest rate.
- Simple interest, once credited, does not earn interest on itself. It remains fixed over time.
- The formula to calculate simple interest is
SI = {(P x R x T)/ 100}
Where,
P = Principal Sum (the original loan)
R = rate of interest (at which the loan is charged)
T = time period (the duration for which money is borrowed) - So, if P amount is borrowed at the rate of interest R for T years then the amount to be repaid to the lender will be
A = P + S.I ,
where S.I = Simple Interest
and A is the amount to be repaid at the end of T years, and is a sum of the principle and interest rate. - Consider a basic example of SI to understand the application of above formula:
Example: Find the simple interest on ₹68000 at 20% p.a. for 2 Years.
Here, P = ₹68000
R = 20 %
T = 2 years
S.I = (68000 x 20 x 1)/100 = ₹13600
Useful Results based on Simple Interest
Have a look at the table below for some useful results based on simple interest and their applications:


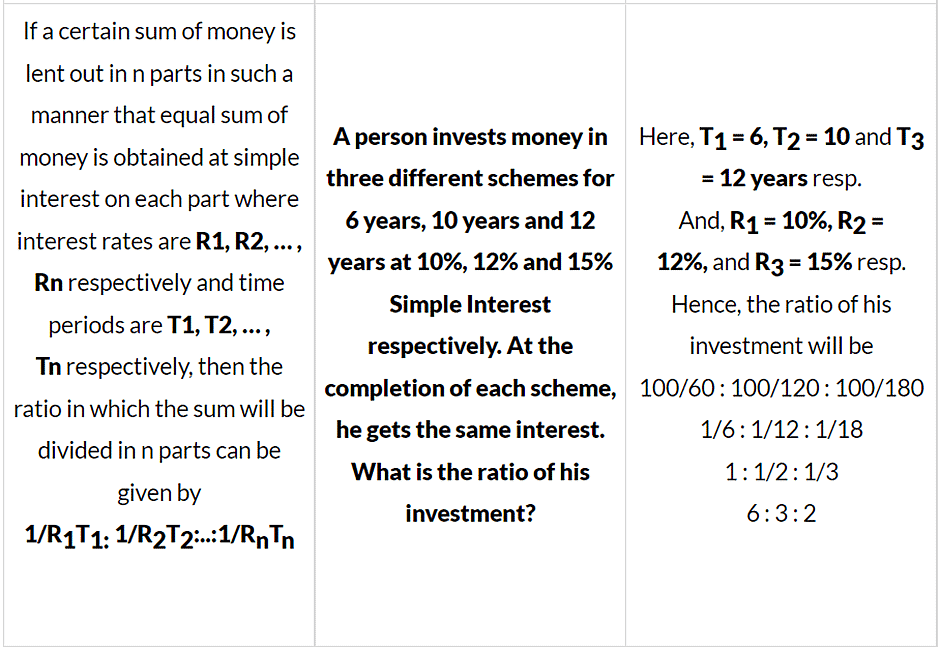
Solved examples on Simple Interest
Que 1: Nitu has an initial capital of ₹20,000. Out of this, she invests ₹8,000 at 5.5% in bank A, ₹5,000 at 5.6% in bank B and the remaining amount at x% in bank C, each rate being simple interest per annum. Her combined annual interest income from these investments is equal to 5% of the initial capital. If she had invested her entire initial capital in bank C alone, then her annual interest income, in rupees, would have been:
a. 700
b. 800
c. 900
d. 1000
Sol: Option 'b' is correct.
Explanation: It is given
Que 2: Mr. Pinto invests one-fifth of his capital at 6%, one-third at 10% and the remaining at 1%, each rate being simple interest per annum. Then, the minimum number of years required for the cumulative interest income from these investments to equal or exceed his initial capital is ____________.
Sol:Let the total investment me 15x and the no. of years required be T years
Que 3: Alex invested his savings in two parts. The simple interest earned on the first part at 15% per annum for 4 years is the same as the simple interest earned on the second part at 12% per annum for 3 years. Then, the percentage of his savings invested in the first part is:
a. 37.5%
b. 62.5%
c. 60%
d. 40%
Sol: Option 'b' is correct.
Explanation: Let the savings invested in first part and second part be 'x' and 'y', respectively.
It is given,
Compound Interest
- This the most usual type of interest that is used in the banking system and economics. In this kind of interest along with one principal further earns interest on it after the completion of 1-time period.
- Suppose an amount P is deposited in an account or lent to the borrower that pays compound interest at the rate of R% p.a. Then after n years the deposit or loan will accumulate to:
P(1+R/100)n - Consider this example, if an amount of 100 is deposited in saving bank account for 3 years at the interest rate of 6% p.a.
- Then, after one year the ₹100 will accumulate to ₹106. Since in compound interest, interest itself earns interest, therefore, after 1-year interest for the 2nd will be calculated on ₹106 unlike to that of Simple interest where interest will be calculated on ₹100 only.
- Thus, after the end of the third year the total amount will become ₹100(1.06)3 = ₹119.1016.
Compound Interest Installment
Let a person takes a loan from the bank at r% and agrees to pay the loan back in equal installments for n years. Then, the value of each installment is given byP = X/ (1 + r/100)n………X/ (1 + r/100)2 + X/ (1 + r/100)
Example: One can purchase a flat from a house building society for ₹ 55000 or on the terms that he should pay ₹ 4275 as cash down payment and the rest in three equal installments. The society charges interest at the rate 16% p.a. compounded half-yearly. If the flat is purchased under an installment plan, find the value of each installment.
Sol: The cost of the flat is ₹ 55000. Now, if the person could either buy flat by paying ₹55000 or through installment plan.
Since the flat was purchased through installment plan then the loan amount = ₹55000 – 4275 (down payment) = ₹50725.Here r = 16% compounded Half-yearly in 3 equal instalments.
Let x be the amount of installment.Then, ₹50725 = x/ (1 + 16/200)3 + x/ (1 + 16/200)2 + x/ (1 + 16/200)
₹50725 = x (1/1.2591 + 1/1.1664 + 1/1.08)
₹50725 = x (0.79421 + 0.85722 + 0.9259)
₹50725 = x (2.577)
₹50725/2.5777 = xx = ₹19683
Important Formulas
- When the interest is compounded Annually:
Amount = P (1 + R/100) n - When the interest is compounded Half-yearly:
Amount = P (1 + (R/2)/100)2n - When the interest is compounded Quarterly:
Amount = P (1 + (R/4)/100)4n - When the rates are different for different years, say R1%, R2% and R3% for 1 year, 2 years and 3-year resp. Then,
Amount = P (1 + R1/100) (1 + R2/100) (1 + R3/100) - Present worth of ₹ x due n years hence is given by:
Present worth = x/ (1 + R/100)n - If a certain sum becomes “x” times in n years, then the rate of compound interest will be R = 100(x1/n – 1)
- If a sum of money P amounts to A1 after T years at CI and the same sum of money amounts to A2 after (T + 1) years at CI, then
R = (A2 – A1)/ A1 x 100
Solved Examples on Compound Interest
Example 1: A man invests ₹ 5000 for 3 years at 5% p.a. compounded interest reckoned yearly. Income tax at the rate of 20% on the interest earned is deducted at the end of each year. Find the amount at the end of the third year.
Sol: Here, P = ₹5000, T = 3 years, r = 5%.
Therefore, Interest at the end of 1st year = 5000 (1 + 0.05) – 5000 = ₹250Now Income tax is 20% on the interest income so the leftover interest income after deducing income tax = (1 – 0.2) * 250 = ₹200
Total Amount at the end of 1st year = ₹5000 + 200 = ₹5200Interest at the end of 2nd year = 5200 (1 + 0.05) – 5200 = ₹260
Interest income after Income tax = 0.8 * ₹260 = ₹208
Total Amount at the end of 2nd year = ₹5200 + 208 = ₹5408Interest at the end of 3rd year = ₹5408 (1.05) – 5408 = ₹270.4
Interest income after Income tax = 0.8 * ₹270.4 = ₹216.32
Total Amount at the end of 2rd year = ₹5408 + 216.32 = ₹5624.32
Example 2: A sum of ₹12000 deposited at compound interest becomes double after 5 years. After 20 years, how much will it become?
Sol: Principal, P = Rs. 12000;
Rate of interest = r%;
Number of years, n = 5;
Amount, A = Rs (2 × 12000) = Rs. 24000
According to the question,
24000 = 12000 × (1 + r/100)5
⇒ (1 + r/100)5 = 2 ...(i)For next part,
Principal, P = Rs. 12000;
Rate of interest = r%;
Number of years, n = 20;
Amount = Rs. x
According to the question,
x = 12000 × (1 + r/100)20
⇒ x = 12000 × (1 + r/100)5 × 4
⇒ x = 12000 × [(1 + r/100)5]4
⇒ x = 12000 × 24 ...[from (i)]
⇒ x = 192000
∴ After 20 years it will become Rs. 1,92,000Shortcut Trick
12000 becomes twice in 5 years = 12000 × 2 = 24000
After another 5 years = 24000 × 2 = 48000
After another 5 years = 48000 × 2 = 96000
After another 5 years = 48000 × = 1,92,000
∴ After 20 years sum will be = 192000
Example 3: John borrowed Rs. 2,10,000 from a bank at an interest rate of 10% per annum, compounded annually. The loan was repaid in two equal instalments, the first after one year and the second after another year. The first instalment was interest of one year plus part of the principal amount, while the second was the rest of the principal amount plus due interest thereon. Then each instalment is Rs _________?
Sol: We have to equate the installments and the amount due either at the time of borrowing or at the time when the entire loan is repaid.
Let us bring all values to the time frame in which all the dues get settled, i.e, by the end of 2 years.
John borrowed Rs. 2,10,000 from the bank at 10% per annum.
This loan will amount to 2,10,000*1.1*1.1 = Rs.2,54,100 by the end of 2 years.
Let the amount paid as installment every year be Rs. x.
John would pay the first installment by the end of the rest year.
Therefore, we have to calculate the interest on this amount from the end of the first year to the end of the second year.
The loan will get settled the moment the second installment is paid.
=> 1.1x + x = 2,54,100 2.1x = 2,54,100
=> x = Rs. 1,21,000.
Therefore, 121000 is the correct answer.
Example 4: Gopal borrows Rs. X from Ankit at 8% annual interest. He then adds Rs. Y of his own money and lends Rs. X+Y to Ishan at 10% annual interest. At the end of the year, after returning Ankit’s dues, the net interest retained by Gopal is the same as that accrued to Ankit. On the other hand, had Gopal lent Rs. X+2Y to Ishan at 10%, then the net interest retained by him would have increased by Rs. 150. If all interests are compounded annually, then find the value of X + Y.
Sol: Amount of interest paid by Ishan to Gopal if the borrowed amount is Rs. (X+Y) = 100 ∗ 10 (X+Y) = 0.1(X+Y)
Gopal also borrowed Rs. X from Ankit at 8% per annum.
Therefore, he has to return Ankit Rs. 0.08X as the interest amount on borrowed sum.
Hence, the interest retained by gopal = 0.1(X+Y) - 0.08X = 0.02X + 0.1Y ... (1)
It is given that the net interest retained by Gopal is the same as that accrued to Ankit.
Therefore, 0.08X = 0.02X + 0.1Y ⇒ X = (5/3)Y0 ... (2)
Amount of interest paid by Ishan to Gopal if the borrowed amount is Rs. (X+2Y)
= 100 ∗ 10 (X+2Y) 0.1X+0.2Y
In this case the amount of interest retained by Gopal = 0.1X+0.2Y - 0.08X = 0.02X + 0.2Y ... (3)
It is given that the interest retained by Gopal increased by Rs. 150 in the second case.
⇒ (0.02X + 0.2Y) - (0.02X + 0.1Y) = 150 Y
= Rs. 1500
By substituting value of Y in equation (2), we can say that
X = Rs. 2500 Therefore, (X+Y) = Rs. 4000
Depreciation of Value
The value of machine or any other article subject to wear and tear decreases with time.
This decrease is called Depreciation.
Thus if A0 is the value at a certain time and r% per annum is the rate of depreciation then the value A1 at the end of t years will be
A1 = A0(1 - r/100)t.
Example 1: The value of the laptop depreciates at the rate of 30 % per annum. The present value of the laptop if Rs. 40000. What will be the worth of laptop two years from now?
a. Rs. 28000
b. Rs 16000
c. Rs. 24400
d. Rs. 19600
Sol: Option 'd' is correct.
Explanation: Here the initial value is given as Rs. 40000,
the rate of interest is 30 % per annum,
the time period is 2 years.
So, the final value,
A1 = 40000 x (1 – 70/100)²
=> 40000 x (0.30)²
=> 19600.
Example 3: The value of a residential flat constructed at a cost of Rs100000 is depreciating at the rate of 10% per annum. What will be its value 3 years after construction?
Sol: The rate of annual growth of population = 5%
We have: V0 (Initial value) = Rs 100000,
R= Rate of depreciation = 10% per annum,
n = 3 years.
Therefore: Value after 3 years will be,
V = 100000 x (1 - 10/100)3
V = 100000 x (9/10 x 9/10 x 9/10)
V = Rs72900
Population Based Question
It has been observed that the population of a specific locale/nation/etc. increases or decreases successively over its previous value,i.e., it increases or decreases like compound interest for money.
Consequently, we use comparable formulas to calculate population.
Let
P1 = Final population after increase/decrease
P0 = Initial Population or Present population
r% = rate at which increase or decrease is happening
When population increases,
P1= P0(1 + r/100)n
When population decreases,
P1= P0(1- r/100)n
Example 1 : The population of a town is 125000. It is increasing at the rate of 2% per annum. What will be its population after 3 years ?
Sol: Present population (P0) = 125000
Rate of increasing (R)=2%
Period (n) = 3 years
∴ Population after 3 years = P1
P1= 125000(1+2/100)3
= 125000(102/100 x 102/100 x 102/100)
P1 = 132651
Example 2: The rate of annual growth of population is 5%. If the present population of a city is 140000, then after three years the population of that city will be approximately?
a. 153000
b. 164000
c. 162000
d. 134000
Sol: Option 'c' is correct
Explanation: The rate of annual growth of population = 5%
The present population of a city = 140000
Formula used: Population of town = P(1+r/100)
According to the question Population of town after three years = P(1+r/100)
=140000(1+5/100)3
= 140000(105/100)3
= (140000 × 21/20 × 21/20 × 21/20)
= (1296540/8)
= 162067.5 ∼ 162000
The required population after three years is 162000
Example 3: The population of the city is increasing at the rate of 8%. If the current population of the city is 100000 then what will be the population after 2 years?
a. 115540
b. 126440
c. 116640
d. 126640
Sol: Option 'c' is correct
Explanation: Principal, P = 10000
Rate, R = 8%
Time, n = 2 years
A = 100000 * (1 + 8/100)2
A= 100000 x (108/100) × (108/100)
A = 116640
The population after 2 years will be 116640.
|
191 videos|131 docs|110 tests
|
FAQs on Basic Concepts: Simple Interest & Compound Interest - Quantitative Aptitude (Quant) - CAT
| 1. What is the difference between simple interest and compound interest? |  |
| 2. How do you calculate simple interest? |  |
| 3. What is the formula for compound interest? |  |
| 4. How does depreciation affect the value of an asset over time? |  |
| 5. How can population growth be modeled using compound interest concepts? |  |

|
Explore Courses for CAT exam
|

|
























